Sainmhíniú agus Foirmle
Anmodúl fearasIs paraiméadar bunúsach é i ndearadh giaranna a shainmhíníonn méid fiacla an ghiar. Ríomhtar é mar an gcóimheas idir anpáirc chiorclach(an fad idir pointí comhfhreagracha ar fhiacla cóngaracha feadh an chiorcail pháirce) go dtí an tairiseach matamaiticiúilπ (pí)De ghnáth, léirítear an modúl i milliméadair (mm).

Cá háit:
● m = modúl giaranna
● cp = páirc chiorclach
Príomhfheidhmeanna an Mhodúil Ghearáin
1. Caighdeánú:
Caighdeánaíonn an modúl toisí fearas, rud a chuireann comhoiriúnacht, inmhalartaitheacht agus éascaíocht olltáirgeadh ar chumas.
2. Cinneadh Neart:
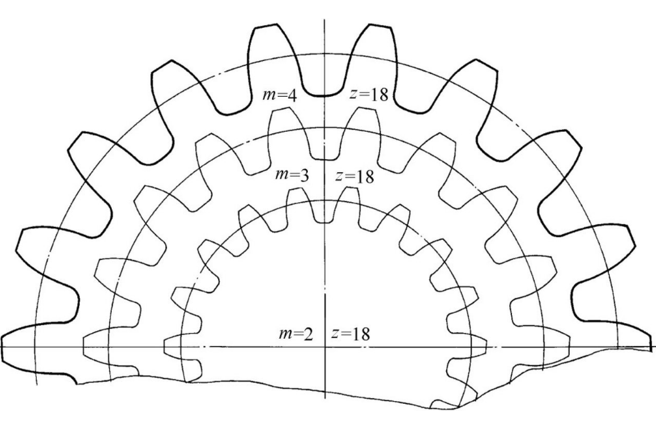
Bíonn tionchar díreach ag an modúl ar thiús agus neart fiacla an ghiar. Mar thoradh ar mhodúl níos mó bíonn fiacla níos láidre ann, atá in ann ualaí níos airde a láimhseáil.
3. Tionchar Toiseach:
Bíonn tionchar aige ar thoisí criticiúla fearas amhail antrastomhas seachtrach, airde na fiacla, agustrastomhas fréimhe.
Critéir Roghnúcháin Modúl
●Riachtanais Luchtaithe:
Éilíonn ualaí meicniúla níos airde modúl níos mó chun neart agus marthanacht leordhóthanach a chinntiú.
●Breithnithe Luas:
I gcás feidhmchlár ardluais, amodúl níos lúis fearr chun fórsaí táimhe a íoslaghdú agus torann a laghdú.
●Srianta Spáis:
● I ndearaí dlútha nó spás teoranta, amodúl níos lúceadaíonn sé méid foriomlán an fhearais a laghdú agus feidhmiúlacht á cothabháil ag an am céanna.
Méideanna Caighdeánacha Modúl
Áirítear ar luachanna modúl caighdeánaithe coitianta:
0.5, 0.8, 1, 1.25, 1.5, 2, 2.5, 3, 4, 5, 6, 8, 10, 12, 16, 20, 25, 32, 40, 50, srl.
Sampla Ríomha
Más é an pháirc chiorclach cpcpcp6.28 mm, ríomhtar an modúl giar mmm mar:
m=6.28π≈2 mm = \frac{6.28}{\pi} \approx 2\ \text{mm} m=π6.28≈2 mm
Achoimre
Is paraiméadar dearaidh ríthábhachtach é an modúl fearas a théann i bhfeidhm ar anméid, neart, agusfeidhmíochtgiar. Cinntíonn roghnú an mhodúil chuí feidhmiúlacht, iontaofacht agus comhoiriúnacht is fearr bunaithe ar éilimh shonracha an fheidhmchláir, lena n-áirítear ualach, luas agus teorainneacha spáis.
Am an phoist: 9 Bealtaine 2025